
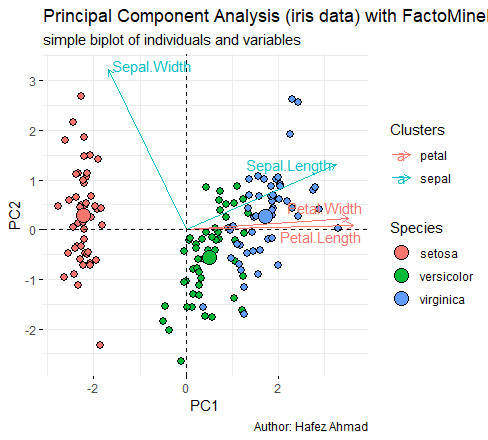
PC2 is highly negatively correlated with Sepal Width.īi plot is an important tool in PCA to understand what is going on in the dataset.ĭifference between association and correlation Prediction with Principal Components trg <- predict(pc, training)Īdd the species column information into trg. PC1 explains about 73.7% and PC2 explained about 22.1% of variability.Īrrows are closer to each other indicates the high correlation.įor example correlation between Sepal Width vs other variables is weakly correlated.Īnother way interpreting the plot is PC1 is positively correlated with the variables Petal Length, Petal Width, and Sepal Length, and PC1 is negatively correlated with Sepal Width. G <- g + theme(legend.direction = 'horizontal', Share point and R Integration library(devtools) Now the correlation coefficients are zero, so we can get rid of multicollinearity issues.
R pca column Pc#
Let’s create the scatterplot based on PC and see the multicollinearity issue is addressed or not?. In this case, the first two components capture the majority of the variability. The first principal components explain the variability around 73% and its captures the majority of the variability. Naïve Bayes Classification in R summary(pc) , p=4):įor example, PC1 increases when Sepal Length, Petal Length, and Petal Width are increased and it is positively correlated whereas PC1 increases Sepal Width decrease because these values are negatively correlated. While printing pc you will get standard deviations and loadings. Scale function is used for normalization pc$scale So we removed the fifth variable from the dataset. Principal Component Analysis is based on only independent variables. One way handling these kinds of issues is based on PCA.Ĭluster optimization in R Principal Component Analysis So if we predict the model based on this dataset may be erroneous. Same way sepal length and petal length, Sepeal length, and petal width are also highly correlated. Petal length and petal width are highly correlated. Lower triangles provide scatter plots and upper triangles provide correlation values. KNN Machine Algorithm in R pairs.panels(training,īg = c("red", "yellow", "blue"), Let’s remove the factor variable from the dataset for correlation data analysis.
Testing <- iris Scatter Plot & Correlations library(psych)įirst will check the correlation between independent variables. Lets divides the data sets into training dataset and test datasets.Įxploratory Data Analysis in R set.seed(111) Sepal.Length Sepal.Width Petal.Length Petal.Width Species In this datasets contains 150 observations with 5 variables.
$ Species : Factor w/ 3 levels "setosa","versicolor".: 1 1 1 1 1 1 1 1 1 1. Self Organizing Maps Getting Data data("iris")ĭata.frame’: 150 obs. In this tutorial we will make use of iris dataset in R for analysis & interprettion. Reducing the number of variables from a data set naturally leads to inaccuracy, but the trick in the dimensionality reduction is to allow us to make correct decisions based on high accuracy.Īlways smaller data sets are easier to explore, visualize, analyze, and faster for machine learning algorithms. The principal components are often analyzed by eigendecomposition of the data covariance matrix or singular value decomposition (SVD) of the data matrix. The first principal component can equivalently be defined as a direction that maximizes the variance of the projected data. PCA commonly used for dimensionality reduction by using each data point onto only the first few principal components (most cases first and second dimensions) to obtain lower-dimensional data while keeping as much of the data’s variation as possible. PCA is used in exploratory data analysis and for making decisions in predictive models.


 0 kommentar(er)
0 kommentar(er)
